In the context of my final year internship at Tweag, I’ve had the opportunity to work on the Glasgow Haskell Compiler (GHC), in an attempt to speed up compile times. GHC is renowned for many things, but compilation speed isn’t one of them. One specific problem exposed in issue #20264 is that in Core, GHC’s intermediate representation, types are systematically inlined, resulting in large type trees having to be traversed and transformed along the pipeline. This blog post aims to explain why this is the case, in which situations it can result in slow compile times and large memory usage, and what we can do about it.

The problem

Let’s take the example from the motivating issue #20264. If you’ve ever played with Haskell’s more advanced type system features, you might have encountered the following type of heterogeneous lists.

type HList :: [Type] -> Type
data HList tys where
  HNil :: HList '[]
  HCons :: forall a as. a -> HList as -> HList (a ': as)

Consider now any literal heterogeneous list, such as foo = HCons 42 (HCons True (HCons 'x' HNil)). Once elaborated into Core, all (implicit) type arguments will be inferred and inserted into the term:

foo :: HList [Int, Bool, Char]
foo = HCons @Int @[Bool, Char] 42
       (HCons @Bool @[Char] True
         (HCons @Char @'[] 'x'
           HNil))

As you can see, the tails repeat for every application of HCons. A four-element list isn’t what’s going to lead to memory explosion, but the important thing to note is that it grows quadratically.

Sharing in Core syntax

Sharing by reference

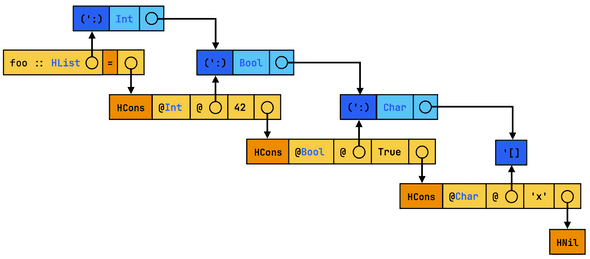
In Haskell, values are boxed by default, which means most data (including Core syntax nodes) is heap-allocated and is passed around by reference instead of by copy. This lets us share common syntax nodes in the intermediate representation. To visualize this sharing, we’re going to use directed graphs where vertices (contiguous boxes) represent syntactic nodes, and arrows are references to these nodes. The best we can hope for in the example above is the following diagram:

However, Haskell is also immutable by default, so if we’re not careful, transforming Core will involve cloning the entire syntax tree in the process. Going back to our example, now on the complete opposite end of the spectrum, this worst-case sharing situation is closer to our initial textual Core representation:

The reality is somewhere in between, depending on how the intermediate representation was generated. Let’s say that the current expression foo was produced by inlining:

bar :: HList as -> HList (Int ': Bool ': as)
bar xs = HCons 42 (HCons True xs)

baz :: HList [Char]
baz = HCons 'x' HNil

foo :: HList [Int, Bool, Char]
foo = bar baz

Desugaring reveals that the type variable as of bar occurs twice in its body:

bar :: forall (as :: [Type]). HList as -> HList (Int ': Bool ': as)
bar = \ @(as :: [Type]) (xs :: HList as) ->
        HCons @Int @(Bool ': as) 42
          (HCons @Bool @as True
            xs)

baz :: HList [Char]
baz = HCons @Char @'[] 'x' HNil

foo :: HList [Int, Bool, Char]
foo = bar @[Char] baz

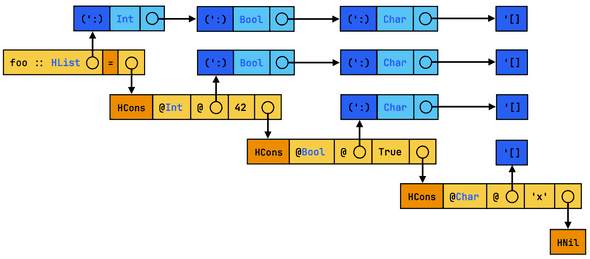
When inlining, GHC substitutes the parameters of bar into the body, replacing occurrences by references to the same memory location. While the textual Core representation is the same as before, the occurrences of as will translate into sharing in the memory representation:

Sharing with variables

In fact, inlining can be decomposed into two intermediate steps: first, the function to be inlined is replaced with its definition; then, if it was a lambda, the now visible function application is $\beta$-reduced by the simplifier, the main driver of Core optimisations. Traditionally, $\beta$-reduction is the process of transforming expressions of the form (\x -> body) arg into body where all occurrences of x in body have been substituted by arg. If x occurs several times in body, then we’ll end up duplicating the contents of arg. Fortunately, GHC’s substitution implementation makes sure we replace every occurrence of x by the same reference to arg. But as we’ve seen these references might be transformed later ultimately leading to actual duplication.

To avoid this problem, GHC instead turns (\x -> body) arg into let x = arg in body instead. Note that x appears several times in body while arg still appears once. This gives us more control on when we’d actually want to substitute arguments. So, at some point in the simplifier pipeline, foo’s Core representation will actually be closer to this:

foo :: HList [Int, Bool, Char]
foo = let @as = TYPE: [Char] in
      let xs = HCons @Char @'[] 'x' HNil in
      HCons @Int @(Bool ': as) 42
       (HCons @Bool @as True
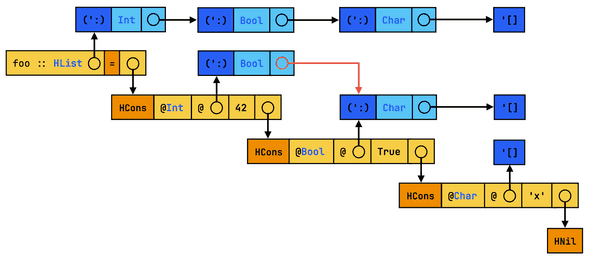
         xs)

When simplifying, GHC returns expressions together with a heap of bindings to be inserted later to the outermost scope. This process is referred to as “let-floating”. Without loss of information, we can ignore those let-bindings and focus on the underlying expression:

The structure is exactly the same as before, but we have replaced some of our references (drawn as circles) by variables (drawn as labelled square boxes). What difference does it make? Well, this kind of sharing is observable, by which I mean it’s embedded inside the intermediate representation. From the compiler’s perspective, variable references are part of the syntax, which can be optimised in many of the same ways that term bindings can. Internally, let-bound variables contain their definition, so our original reference is still there. But unlike raw references, which only exist inside GHC’s running memory, using let-bound variables makes sharing serialisable, being able to live beyond a single GHC invocation.

From references to variables and back

Inlining

Taking a step back, let’s ask ourselves why would types be more subject to size explosion compared to terms. At the end of the day what GHC really cares about is runtime performance. Carelessly inlining might duplicate runtime work. Instead, the inliner attempts to find a equilibrium between code performance and binary size. But types don’t count in the final binary size: they are erased, so there’s no reason not to inline them, at least regarding runtime performance. For this reason, GHC substitutes type-lets without exception, unlike term-level let-bindings which tend to be inlined if they’re small or used once, as well as other criteria that are less applicable to types.

What we actually want is rather an equilibrium between code performance and code size at all steps of the pipeline. With this in mind, it makes sense to prevent some types from being inlined as well. Instead of preventing some inlinings to mitigate binary size, we care more generally about code size and hence type sizes, including in the intermediate representation.

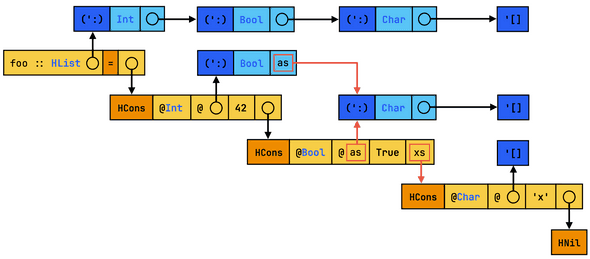
Diagrammatically, inlining/substituting can be viewed as replacing boxes with circles. As we inline, we effectively replace all occurrences of a variable with references to the same syntax node allocation. We’ve seen this systematically happens for type applications: instead of generating a let-binding, the type variable gets immediately substituted. A first solution to this problem is to delay inlining of types as much as possible, in order to keep as many variable references as possible.

Since type-lets are already supported in the syntax of Core, the implementation consists in simply avoiding substitution when encountering them, unless the variable occurs once or is bound to a small type. But as type-lets survive longer in the pipeline, many existing core transformations crash when traversing type-lets, as they currently only expect term-level bindings, notably at the top-level. Most of the difficulty comes from identifying the root cause of such situations.

ANF-conversion

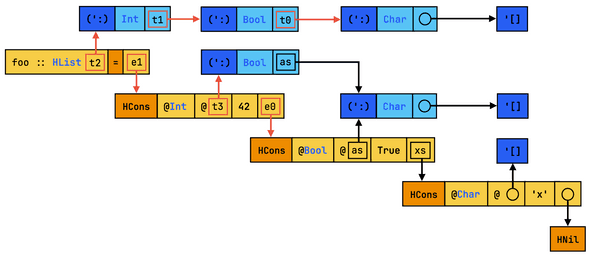
If inlining corresponds to turning variables into references, ANF-conversion corresponds to the reverse transformation. ANF, short for A-normal form, is a restriction on syntax that imposes call arguments to be atomic in the sense that their syntax tree has a depth of 1. To do so, non-trivial arguments are recursively turned into ANF and let-bound. Going back to our toy example, ANF-conversion would result in the following Core program:

@t0 :: [Type]
@t0 = TYPE: [Char]

@t1 :: [Type]
@t1 = TYPE: Bool ': t0

@t2 :: [Type]
@t2 = TYPE: Int ': t1

foo :: HList t1
foo = let @as = TYPE: [Char] in
      let xs = HCons @Char @'[] 'x' HNil in
      let e0 = HCons @Bool @as True xs in
      let @t3 = TYPE: Bool ': as
      let e1 = HCons @Int @t3 42 e0 in
      e1

And here’s the corresponding diagram:

ANF-conversion is already done in Core, but only for terms. A second piece of the solution is therefore to convert types into A-normal form as well. In practice, GHC splits this pass in two, first replacing non-trivial arguments e to let x = e in x, and then floating-out accordingly.

In fact, during typechecking, types are sprinkled in expressions and typing constraints in a way that resembles A-normal form:

baz :: t0
baz = HCons @t1 @t2 'x' HNil

-- Constraints
t0 ~ HList t3
t1 ~ Char
t2 ~ '[]
t3 ~ t1 ': t2

Once solved, these type variables are substituted into baz, in a process known as zonking:

baz :: HList [Char]
baz = HCons @Char @'[] 'x' HNil

What if we use instead let-bindings for each of the solved type variables?

@t0 :: Type
@t0 = TYPE: HList t3

baz :: t0
baz =
  let @t1 = TYPE: Int
      @t2 = TYPE: '[]
      @t3 = TYPE: t1 ': t2
  in HCons @t1 @t2 'x' HNil

By doing so, ANF emerges naturally, and the resulting sharing reflects actual typing constraints. Having explainable ANF is desirable at such an early stage of the pipeline. This process happens before Core is even generated, so before all Core transformations even have a chance to destroy sharing!

Common subexpression elimination

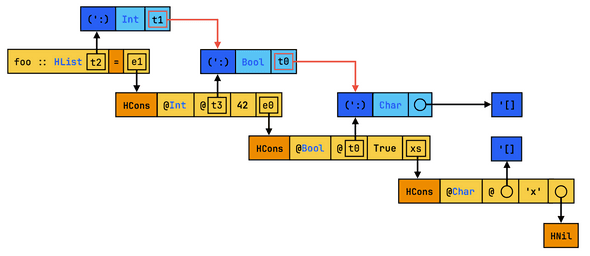
In the previous paragraph I explained how to introduce variable sharing a priori: when zonking, we know from the typechecker that different unification variables resolve to the same type. But we also want to introduce this sharing a posteriori; that is we want to look for identical syntax trees and have them point to the same variable. This process is referred to as common subexpression elimination (CSE), yet another pass that is performed for terms but not types! If we perform CSE on types as well, our running example would result in the following:

@t0 :: [Type]
@t0 = TYPE: [Char]

@t1 :: [Type]
@t1 = TYPE: Bool ': t0

@t2 :: [Type]
@t2 = TYPE: Int ': t1

foo :: HList t1
foo = let xs = HCons @Char @'[] 'x' HNil in
      let e0 = HCons @Bool @t0 True xs in
      let e1 = HCons @Int @t1 42 e0 in
      e1

The result is essentially the same as our initial best-case sharing scenario:

CSE is not only meant to optimise the program being compiled but also the compiler itself, as we’re decreasing the code size, reducing work in future transformations. By doing the same for types, which are static data, we don’t optimise the program at all, but only the compiler.

Conclusion

We’ve seen that changing the kind of indirection being used in intermediate syntax can result in a shift of perspective. Instead of sharing by using meta-level indirections (references in GHC’s memory), we’re using object-level indirections (variables in the intermediate representation). Certain program transformations such as inlining and ANF-conversion can be understood as inverses, swapping the kind of indirection while preserving the in-memory structure. Embedding sharing inside the intermediate representation gives us an opportunity to apply term-level optimisations at the type-level as well. Notably, let-floating and common subexpression elimination enable smaller program sizes (which includes type sizes) and as a result speeds up later transformations.

The implementation falls out nicely in the current GHC pipeline, and amounts to extending existing passes for types. Most of what has been described in this post is still being worked on, in the meantime I have opened a merge request on which you can follow its progress. In the current version of GHC, the only source of type-lets is $\beta$-reduction. For now, the MR focuses on trying to make these let-bound types variables survive as long as possible in the pipeline. To inline single-occurring type variables, I have implemented precise occurrence analysis for types. Even at this stage, let-floating is a requirement, if we float term-lets but not type-lets, then the types of those term-level bindings might refer to out of scope type variables. However ANF-isation and CSE are independent from the other passes, so I chose to integrate them later in the MR. Experimenting in a separate branch reveals they’re easily implemented by reusing the term-level logic.

I’d like to thank Tweag for supporting this internship, particularly Yann Hamdaoui and Torsten Schmits for the mentorship along the semester, and Alexis King who proposed this subject. It was a great opportunity to get to know the inner clockwork of GHC and try to contribute to a project I use on a regular basis. I learned a lot trying to work on something as large as GHC, both about compilers and methodology.